Einsendeaufgaben EA-Besprechung 31521 SS 2013 EA2 41520 (08.07.2013)
- Ersteller Antonio
- Erstellt am
Münchner Kindl
Tutorin und Forenadmin
Alte EAs mit Lösungen findet man im Moodle des Moduls Banken und Börsen.
Mein Lösungsvorschlag:
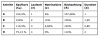
Kapitalmarktzins: r=10%
Teilaufgabe a) siehe EA2 WS 2008/09
A
B
C
D
Teilaufgabe b) siehe EA2 WS 2008/09
bitte ignorieren, richtige Lösung unten in Beitrag 6.
Anleihe A:
Anleihe D und Gesamtrendite:
Teilaufgabe c) siehe EA 2 WS 2010/11 d)
bitte ignorieren, richtige Lösung unten in Beitrag 4.
Teilaufgabe d) siehe EA 2 WS 2010/11 c) und KE4, S.52
Falls die Duration seines Portefeuille aus Wertpapier B und C genau mit seiner geplanten Anlagedauer übereinstimmt, so kann er sich damit gegen die aus der Möglichkeit zwischenzeitlicher Zinsänderungen resultierenden Risiken annähernd immunisieren:
x: Anteil des Wertpapiers B am Portefeuille
1-x: Anteil des Wertpapiers C am Portefeuille
geplante Anlagedauer: 2 = gewünschte Duration
→ 2 = x∙dB + (1-x) ∙dC
⇔ 2 = 1,9x + 2,8(1-x)
⇔ x =0, = 88,89%
→ 1-x = 0, = 11,11%
Der Anteil von Wertpapier B am Portefeuille: 88,89%, während der Anteil Wertpapier C am Portefeuille 11,11% ist:
Teilaufgabe e)
Nur beim Zero-Bond ist die Duration identisch mit der Restlaufzeit.
Teilaufgabe f)
Ja, das stimmt.
Quelle: siehe S. 3, Zeile 20 hier
Teilaufgabe g)
Nein, je höher der Wert der Duration ist, desto höher sind Zinssensitivität und Zinsänderungsrisiko.
Quellen:
Teilaufgabe h)
Ja, da die Duration der gewichtete Mittelwert der Zeitpunkte ist, zu denen der Anleger Zahlungen aus einem Wertpapier erhält, erhält der Anleger bei einer kürzeren Duration Teile seines Kapitals früher zurück als bei einer längeren Duration.
Im Extremfall des Zero-Bonds erhält er sein Kapital in einem Stück erst ganz am Ende der Laufzeit zurück.
Quelle: siehe letzten 3 Zeilen hier
Mein Lösungsvorschlag:
Kapitalmarktzins: r=10%
Teilaufgabe a) siehe EA2 WS 2008/09
A
B
C
D
Teilaufgabe b) siehe EA2 WS 2008/09
bitte ignorieren, richtige Lösung unten in Beitrag 6.
Anleihe A:
Anleihe D und Gesamtrendite:
Teilaufgabe c) siehe EA 2 WS 2010/11 d)
bitte ignorieren, richtige Lösung unten in Beitrag 4.
Teilaufgabe d) siehe EA 2 WS 2010/11 c) und KE4, S.52
Falls die Duration seines Portefeuille aus Wertpapier B und C genau mit seiner geplanten Anlagedauer übereinstimmt, so kann er sich damit gegen die aus der Möglichkeit zwischenzeitlicher Zinsänderungen resultierenden Risiken annähernd immunisieren:
x: Anteil des Wertpapiers B am Portefeuille
1-x: Anteil des Wertpapiers C am Portefeuille
geplante Anlagedauer: 2 = gewünschte Duration
→ 2 = x∙dB + (1-x) ∙dC
⇔ 2 = 1,9x + 2,8(1-x)
⇔ x =0, = 88,89%
→ 1-x = 0, = 11,11%
Der Anteil von Wertpapier B am Portefeuille: 88,89%, während der Anteil Wertpapier C am Portefeuille 11,11% ist:
- 13.333,33€ (= 0, ∙15.000€) in Wertpapier B anlegen, und
- 1.666,67€ (= 0, ∙15.000€) in Wertpapier C anlegen.
Teilaufgabe e)
Nur beim Zero-Bond ist die Duration identisch mit der Restlaufzeit.
Teilaufgabe f)
Ja, das stimmt.
Quelle: siehe S. 3, Zeile 20 hier
Teilaufgabe g)
Nein, je höher der Wert der Duration ist, desto höher sind Zinssensitivität und Zinsänderungsrisiko.
Quellen:
- "Je höher die Duration, desto höher ist das Zinsänderungsrisiko." hier
- 4. und 5. Zeile von unten, hier.
Teilaufgabe h)
Ja, da die Duration der gewichtete Mittelwert der Zeitpunkte ist, zu denen der Anleger Zahlungen aus einem Wertpapier erhält, erhält der Anleger bei einer kürzeren Duration Teile seines Kapitals früher zurück als bei einer längeren Duration.
Im Extremfall des Zero-Bonds erhält er sein Kapital in einem Stück erst ganz am Ende der Laufzeit zurück.
Quelle: siehe letzten 3 Zeilen hier
Hallo, Ich stimme mit deiner Lösung überein. Nur bei der c) steht doch, dass man anhand von d die absolute und relative Kursänderung bestimmen soll. So Hab ich zuerst b berechnet mit b=d/(1+r) und damit b=2,8/1,105=2,534. Damit kann man dann a berechnen durch a=b*C=2,534*110,5%=1940. Oder Hab ich da jetzt einen Denkfehler??? 
Münchner Kindl
Tutorin und Forenadmin
Teilaufgabe c) korrigiert:
Ja, weiß der Geier warum ich es damals nicht einfach so gerechnet habe
In der Teilaufgabe d) der EA 2 WS 2010/11 (die ich ja als Quelle angegeben hatte, also hatte ich sie mir wohl auch angeschaut) wird es ja mit d und b gelöst:
Approximierte Kursänderung:
r= 10% = 0,1
Duration des Wertpapiers C aus Teilaufgabe a): d = 2,8042
→ b = $\frac{d}{1+r} = \frac{2,8042}{1,1}$ = 2,549272727
mit $\Delta r$ = 10,5% - 10% = 0,5% = 0,005
$\frac{\Delta C_0}{C_0} = -b·\Delta r$= -2,549272727·0,005 = -0,0127 = 1,27%
mit C0 = 110,5% von 1.000€ = 1.105€:
→ $\Delta C_0 = \frac{\Delta C_0}{C_0}·C_0$ = -0,0127·(110,5%·1.000€) = -0,0127·1.105€= -14,08473€ = -14,08€
Tatsächliche Kursänderung:
Am Ende der 3-jährigen Laufzeit steht die Anleihe zu 120%, d.h. bei 1.200€ (da der Nominalwert der Anleihe 1.000€ war!).
Jetzt zinst man den Endwert 1.200€ und die jährlichen Zinszahlungen von 68,17€ (da z= 6,817%, und der jährliche Zins 6,817% des Nominalwerts 1.000€ ist) ab, um die Kaufkurse C0 in Abhängigkeit der Zinssätze r zu berechnen:
C0(r=10%) = $\frac{68,17€}{1,1^1}$ + $\frac{68,17€}{1,1^2}$ + $\frac{68,17€}{1,1^3}$ + $\frac{1.200€}{1,1^3}$ = 1.071,106461€ = 1.071,11€
C0(r=10,5%) = $\frac{68,17€}{1,105^1}$ + $\frac{68,17€}{1,105^2}$ + $\frac{68,17€}{1,105^3}$ + $\frac{1.200€}{1,105^3}$ = 1.057,44191€ = 1.057,44€
→ $\Delta C_0$ = 1.057,44€ - 1.071,11€ = -13,67€
Ja, weiß der Geier warum ich es damals nicht einfach so gerechnet habe
In der Teilaufgabe d) der EA 2 WS 2010/11 (die ich ja als Quelle angegeben hatte, also hatte ich sie mir wohl auch angeschaut) wird es ja mit d und b gelöst:
Approximierte Kursänderung:
d = b·(1+r)
$\frac{\Delta C_0}{C_0} = -b·\Delta r$
$\frac{\Delta C_0}{C_0} = -b·\Delta r$
r= 10% = 0,1
Duration des Wertpapiers C aus Teilaufgabe a): d = 2,8042
→ b = $\frac{d}{1+r} = \frac{2,8042}{1,1}$ = 2,549272727
mit $\Delta r$ = 10,5% - 10% = 0,5% = 0,005
$\frac{\Delta C_0}{C_0} = -b·\Delta r$= -2,549272727·0,005 = -0,0127 = 1,27%
mit C0 = 110,5% von 1.000€ = 1.105€:
→ $\Delta C_0 = \frac{\Delta C_0}{C_0}·C_0$ = -0,0127·(110,5%·1.000€) = -0,0127·1.105€= -14,08473€ = -14,08€
Tatsächliche Kursänderung:
Am Ende der 3-jährigen Laufzeit steht die Anleihe zu 120%, d.h. bei 1.200€ (da der Nominalwert der Anleihe 1.000€ war!).
Jetzt zinst man den Endwert 1.200€ und die jährlichen Zinszahlungen von 68,17€ (da z= 6,817%, und der jährliche Zins 6,817% des Nominalwerts 1.000€ ist) ab, um die Kaufkurse C0 in Abhängigkeit der Zinssätze r zu berechnen:
C0(r=10%) = $\frac{68,17€}{1,1^1}$ + $\frac{68,17€}{1,1^2}$ + $\frac{68,17€}{1,1^3}$ + $\frac{1.200€}{1,1^3}$ = 1.071,106461€ = 1.071,11€
C0(r=10,5%) = $\frac{68,17€}{1,105^1}$ + $\frac{68,17€}{1,105^2}$ + $\frac{68,17€}{1,105^3}$ + $\frac{1.200€}{1,105^3}$ = 1.057,44191€ = 1.057,44€
→ $\Delta C_0$ = 1.057,44€ - 1.071,11€ = -13,67€
Fehlen bei Aufgabe b) nicht die Zinszahlungen, die man erhält?
Münchner Kindl
Tutorin und Forenadmin
Teilaufgabe b) korrigiert:
Ja, stimmt, danke!
A ist ja eine stinknormale Anleihe und keine Nullkuponanleihe wie D, also muß man bei A noch den Zins von5€ 50€ pro Anleihe (= 5% des Nominalwerts 100€ 1.000€) addieren:
Wie viele Stück der Anleihe A kann man für 10.000€ kaufen?
Endwert nach 1 Jahr?
Wie viele Stück der Anleihe D (Nullkuponanleihe) kann man für 10.000€ kaufen?
Endwert nach 4 Jahren?
Endwert nach 1 Jahr, sprich 3 Jahre vor Laufzeitende nach 4 Jahren?
→ Endwert abzinsen um 3 Jahre, mit Marktzins 10%:
Rendite
Ja, stimmt, danke!
A ist ja eine stinknormale Anleihe und keine Nullkuponanleihe wie D, also muß man bei A noch den Zins von
Wie viele Stück der Anleihe A kann man für 10.000€ kaufen?
= $\frac{10.000€}{C_0}$ = $\frac{10.000€}{1,025∙1.000€}$ = 9,76 Anleihen
Endwert nach 1 Jahr?
= EW1 Jahr
= Anzahl_Anleihen∙Rückzahlung + Anzahl_Anleihen∙Zins
= 9,76∙107,38%∙1.000€ + 9,76∙5€50€
=10.524,88€ 10.963,90€
= Anzahl_Anleihen∙Rückzahlung + Anzahl_Anleihen∙Zins
= 9,76∙107,38%∙1.000€ + 9,76∙
=
Wie viele Stück der Anleihe D (Nullkuponanleihe) kann man für 10.000€ kaufen?
= $\frac{10.000€}{C_0}$ = $\frac{10.000€}{0,7513∙1.000€}$ = 13,31 Anleihen
Endwert nach 4 Jahren?
= EW4 Jahre
= Anzahl_Anleihen∙Rückzahlung
= 13,31∙110%∙1.000€
= 14.641,29€
= 13,31∙110%∙1.000€
= 14.641,29€
Endwert nach 1 Jahr, sprich 3 Jahre vor Laufzeitende nach 4 Jahren?
→ Endwert abzinsen um 3 Jahre, mit Marktzins 10%:
= $\frac{EW_{4 Jahre}}{1,1^3}$
= $\frac{14.641,29€}{1,1^3}$
= $\frac{14.641,29€}{1,1^3}$
= 11.000,22€
Rendite
= ( 0,5∙$\frac{10.963,90€}{10.000€}$ + 0,5∙$\frac{11.000,22€}{10.000€}$ ) -1
= 1,076255 1,098206122 - 1
=0,0763 0,0982
=
=7,63% 9,82%
Und jetzt sind es eigentlich 5% von 1000€, nicht 100€. ;)
Münchner Kindl
Tutorin und Forenadmin
Arrgh!!
Da hast Du natürlich recht, immer diese Details
Ich korrigiere es gleich oben.
Da hast Du natürlich recht, immer diese Details
Ich korrigiere es gleich oben.
"welches Endvermögen wird in t=1 realisiert"
Soll man das wörtlich nehmen oder ist das ein spezieller Ausdruck? Soll hier die abgezinste Rückzahlung der D-Anleihe wirklich rein?
edit: Wenn man die Anleihe in t=1 veräußert, würde es passen.
Soll man das wörtlich nehmen oder ist das ein spezieller Ausdruck? Soll hier die abgezinste Rückzahlung der D-Anleihe wirklich rein?
edit: Wenn man die Anleihe in t=1 veräußert, würde es passen.
Münchner Kindl
Tutorin und Forenadmin
Ja, ich hatte mir auch erst überlegt, ob das eine Fangfrage sein soll, da ja der Nullkupon D die 4-jährige Laufzeit hat, aber es dann lieber so gelöst, mit dem Abzinsen, nach dem Motto bei den 10 Punkten für die Teilaufgabe erwarten sie auch viele Rechenschritte