Mein Lösungsvorschlag:
Aufgabe 1
D
E
****
Homogenität:
Q(λL, λC) = λ
h ∙ Q(L, C)

****
A ist falsch:
Q(λL, λC) = $ \frac{(λL)^2 (λC)^2 }{(λL)^3 + (λC)^3} = λ \frac{L^2 C^2 }{L^3 + C^3} $ = λ Q = λ
1 Q
→ sie ist homogen vom Grade 1 = sie weist konstante Skalenerträge auf
****
B ist falsch:
Q(λL, λC) = 3(λL)
2 + (λC)
2 = λ
2 (3L
2 + C
2) = λ
2 Q
→ sie ist homogen vom Grade h=2
****
C ist falsch:
Q(λL, λC) = 3 λ
0,5L
0,5C
0,5 + λL = λ (3L
0,5C
0,5 + L) = λ Q = λ
1 Q
→ sie
ist homogen, und zwar vom Grade 1
****
D ist richtig:
Q(λL, λC) = $ \alpha[\beta \lambda^{-\rho} l^{-\rho} + (1-\beta)c^{-\rho} \lambda^{-\rho}]^{-\frac{1}{\rho}} $ = λ Q = λ
1 Q
****
E ist richtig:
KE3, S. 42
u(x) = v(w(x)) ist eine homothetische Produktionsfunktion, falls:
- w ist eine linear-homogene (d.h. homogen vom Grade 1) Funktion und
- v ist eine streng monoton steigende Funktion, z.B. x2 oder $ \sqrt x $: http://de.wikipedia.org/wiki/Monotonie_(Mathematik), und
- nachträglich ergänzt: u(0) = 0, damit es eine Produktionsfunktion ist (ohne Input, kein Output)
Für unsere Funktion:
- Q(λL, λC) = λα+(1-α)LαC1-α = λ1 LαC1-α = λ1 Q --> linear-homogene Funktion, und
- eQ-1 ist eine streng monoton steigende Funktion, und
- nachträglich ergänzt: F(0)=0 damit es eine Produktionsfunktion ist (ohne Input, kein Output). e0-1= 1-1=0
→ die Funktion ist eine homothetische
Produktionsfunktion.
Aufgabe 2
C
D
****
A ist falsch:
Q = $ \sqrt{10.000 L} = 100 \sqrt{L} = 100 L^{0,5} $
$ \frac{\partial Q}{\partial L} = 0,5·100·L^{-0,5} = 50·L^{-0,5} $
****
B ist falsch:
KE3 S. 16, 18, 20, 22
a) ist richtig
b) ist richtig
c) ist richtig
d) ist falsch. KE3 S. 79 Abbildung A 3.3-20: das ist eine kurzfristige Kostenkurve einer ertragsgesetzlichen Produktionsfunktion.
****
C ist richtig:
KE3, S. 28
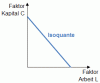
Lineare Produktionsfunktion: Q = αL + βC
Jeder der Faktoren ist vollkommen substituirbar, d.h. daß z.B. Faktor L aus der Produktion sogar vollkommen verdrängt werden kann, man muß nur mehr von dem anderen Faktor C verwenden und man bekommt trotzdem die gleiche Produktmenge Q.
****
D ist richtig:
Falls die Ausgangskombination von Produktionsfaktoren effizient war, z.B. 4 Tischbeine und 1 Platte (soviel braucht man um einen Tisch zu bauen), dann ist auch ein Vielfaches davon effizient, z.B. 20 Tischbeine und 5 Platten (daraus kann man 5 ganze Tische bauen).
****
E ist falsch:
Hier wurde das Nachdifferenzieren bei der Kettenregel vergessen.
$ \frac{\partial Y}{\partial L} = e^{L^\alpha C^{1-\alpha}} \alpha L^{\alpha-1} $
Aufgabe 3
D
****
A ist falsch:
umgekehrt wäre es richtig
****
B ist falsch:
Gleichung umformen:
$ Q = L^\frac{6}{10} C^\frac{4}{10} │()^\frac{10}{6} $
⇔ $ Q^\frac{10}{6} = L C^{\frac{4}{10}\frac{10}{6}} $
⇔ $ Q^\frac{5}{3} C^{-\frac{2}{3}} = L $ Isoquante
Jetzt Steigung der Isoquante berechnen
Q = const. man berechnet die Isoquante für verschiedene Werte der Produktmenge Q:
$ \frac{dL}{dC} = -\frac{2}{3} Q^\frac{5}{3} C^{-\frac{5}{3}} $
****
C ist falsch:
KE3, S. 25
umgekehrt wäre es richtig:
$ \frac{dL}{dC} = - \frac{\frac{\partial Q}{\partial C}}{\frac{\partial Q}{\partial L}} $
****
D ist richtig:
Expansionspfad: geometrischer Ort aller Minimalkostenkombinationen der Produktionsfaktoren Arbeit L und Kapital C.

zu minimieren: Kosten = l·L + r·C mit l=Lohn(stunden)satz und r=Zins
Nebenbedingung: Q = 10 L
0,8C
0,2
→ Lagrange-Funktion aufstellen:
$ \Lambda = l·L + r·C + \lambda·(\overline Q - 10 L^{0,8} C^{0,2}) $
mit $ \overline Q = constant $
I) $ \frac{\partial \Lambda}{\partial L} = l - \lambda · 10 · 0,8 · L^{-0,2}C^{0,2} = 0 $
II) $ \frac{\partial \Lambda}{\partial C} = r - \lambda · 10 · 0,2 · L^{0,8}C^{-0,8} = 0 $
I) umformen: $ \lambda = \frac{l}{8L^{-0,2}C^{0,2}} $
und einsetzen in II): $ r = \frac{l}{8L^{-0,2}C^{0,2}}·2·L^{0,8}C^{-0,8} = \frac{1}{4}l\frac{L}{C}$
Umformen: $ C = \frac{1}{4} \frac{l}{r}L $ das ist eine Gerade durch den Ursprung.
****
E ist falsch:
Der Expansionspfad ist eine Gerade druch den Ursprung (siehe D) und deswegen streng monoton
steigend in
allen Bereichen.
Aufgabe 4
A
E
A ist richtig:
KE3 S. 96 1. Abschnitt, S. 95 2. Aufzählungspunkt
****
B ist falsch:
durchschnittliche fixe Kosten: $ \frac{K_{fix}}{Q} $ sinken, je größer die Produktmenge Q ist.
****
C ist falsch:
es fehlt das Wort "minimal".
Richtig wäre:
Firma stellt die Produktion ein, wenn die minimalen variablen Durchschnittskosten höher sind als der Preis, also der Marktpreis niedriger ist als die minimalen variablen Durchschnittskosten.
KE3, S. 98-100
variable Durchschnittskosten: DK
v = $ \frac{K_{variabel}}{Q} $
KE3 S. 98-99 und Abb. A 3.4-1
bei erzielbarer Produktpreis P <
min(DK
v) → Firma bietet nichts mehr, also sie stellen die Produktion ein
****
D ist falsch:
Für Zeitpunkt der Produktionseinstellung siehe C.
Bei min(DK
v) < P < min(DK) = $ \frac{K}{Q} $ macht die Firma immer noch genug Ertrag um die variablen Kosten und einen Teil der fixen Kosten zu decken.
In anderen Worten, in dem Preisbereich ist der Deckungsbeitrag > 0.
****
E ist richtig:
KE3 S. 101 Abb. 3.4-2
Die Cobb-Douglas-Produktionsfunktion ist eine neoklassische Produktionsfunktion.
Für alle Produktionsfunktionen ist die kurzfristige Angebotskurve gleich der Grenzkostenkurve.
Aufgabe 5
A
B
A ist richtig:
Die Firma würde den Faktor (z.B. L) schon nicht mehr nachfragen falls der Faktorpreis (z.B. Lohnstundensatz) über dem maximalen Durchschnittserlös liegt.
Aber auch die Aussage ist hier ist richtig, da das Maximum der Grenzerlöskurve noch höher ist als das Maximum der Durchschnittserlöskurve wird die Firma bei so einem noch höheren Preis erst recht nicht den Faktor nachfragen.
****
B ist richtig:
KE3, S. 114
Q umformen nach L: Q
2 = LC = 100L --> L = Q
2/100
****
C ist falsch wegen der Produktregel:
Schauen wir den Faktorpreis l and und nehmen wir an, l sei eine Funktion der Faktormenge L: l(L)
Kostenfunktion: K = l(L)·L + r·C
Grenzkosten des Faktors Arbeit L, Berechnung mit Produktregel (u·v)' = u'·v + u·v':
$ \frac{dK}{dL} = \frac{dl(L)}{dL}·L + l(L) $
Gewinn = Ertrag - Kosten
G = P·Q - [l(L)·L + r·$\overline C$]
Gewinnmaximierung:
$ \frac{dG}{dL} = P·\frac{dQ}{dL} - [ \frac{dl(L)}{dL}·L + l(L) ] = 0 $
⇔ $ P·\frac{dQ}{dL} - \frac{dK}{dL} = 0 $
⇔ $ P·\frac{dQ}{dL} = \frac{dK}{dL} = \frac{dl(L)}{dL}·L + l(L) $
****
D ist falsch:
Wie immer geht es Gewinnmaximierung.
Wir suchen die gewinnmaximierende Nachfragefunktion für L, also für welches L der Gewinn maximal wird.
Q ist hier eine neoklassische Cobb-Douglas-Produktionsfunktion.
$ \overline C $ ist kurzfristig konstant, siehe KE3 S. 98, 2. Aufzählungspunkt.
Gewinn = Ertrag - Kosten
G = P·Q - l·L - r·$ \overline C $
$ G = P·10·L^0,5·{\overline C}^{0,5} - l·L - r·\overline C $
$ \frac{dG}{dL} = 0,5·P·10·L^{-0,5}{\overline C}^{0,5} - l = 0 $
⇔ $ 5·PL^{-0,5}{\overline C}^{0,5} = l │·L^0,5 $
⇔ $ 5·P·{\overline C}^{0,5}= l·L^{0,5} $ │ Quadrieren
⇔ $ L = \frac{25P^2·{\overline C}}{l^2} $
d.h. je höher der Lohnstundensatz l ist, desto weniger Arbeit wird die Firma nachfragen. Siehe auch KE3, S. 116, Abb. A 3-5.1 Faktornachfragekurve
⇔ L = 25 mit den Werten aus der Aufgabe
****
E ist falsch:
Aus Berechnung für Teilaufgabe D:
$ L = \frac{25P^2·{\overline C}}{l^2} $
d.h. die kurzfristige Nachfrage nach dem Faktor Arbeit ist abhängig vom Lohnsatz l.
Je höher der Lohnstundensatz l ist, desto weniger Arbeit wird die Firma nachfragen. Siehe auch KE3, S. 116, Abb. A 3-5.1 Faktornachfragekurve


