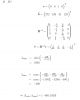App installieren
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Anmerkung: This feature may not be available in some browsers.
- Wirtschaft
- Master Volkswirtschaftslehre
- Wahlpflicht quantitative Mastermodule
- 32621 Optimierungsmethoden des Operations Research
Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Einsendeaufgaben EA-Besprechung | 32621 | SS 2019 | EA1 00851 | 06.06.2019
- Ersteller Antonio
- Erstellt am
Hallo Lisa,
hab mit der EA1 schon angefangen und bin durch.
Meine Ergebnisse zum Abgleich:
Aufgabe 1c) 20 mal B1, 40 mal B2 und 120 mal B3
Aufgabe 1d3) Solange die Backzeit im Intervall [2.75h und 5.375h] bleibt, ist die Basis optimal.
Aufgabe 2b) Die optimale Lösung liegt bei x1 = 3 und x2 = 3, Zielwert ist x0 = 27
Aufgabe 2c) Lösung des dualen LOP: u1 = 1.5, u2 = 1.5, u3 = 0, Zielwert u0 = 27
VG Andreas
hab mit der EA1 schon angefangen und bin durch.
Meine Ergebnisse zum Abgleich:
Aufgabe 1c) 20 mal B1, 40 mal B2 und 120 mal B3
Aufgabe 1d3) Solange die Backzeit im Intervall [2.75h und 5.375h] bleibt, ist die Basis optimal.
Aufgabe 2b) Die optimale Lösung liegt bei x1 = 3 und x2 = 3, Zielwert ist x0 = 27
Aufgabe 2c) Lösung des dualen LOP: u1 = 1.5, u2 = 1.5, u3 = 0, Zielwert u0 = 27
VG Andreas
Hallo Andreas,
bei Aufgabe 2 habe ich die gleichen Ergebnisse wie du. Bei Aufgabe 1 habe ich die Lösung (x1,x2,x3,x4,x5,x6)^T=(0,0,5,135,195,35)^T mit x0=10 erhalten. Wie sieht dein Optimierungsmodell aus? Ich habe mit folgendem gerechnet:
Max x0=1,5x1+2,5x2+2x3
u.d.N.
x1+1,5x2+x3<=5
x1+x3<=140
2x2+x3<=200
x1+x2+x3<=40
x1,x2,x3>=0
M.E. müssen die Restriktionen zu Hefe, Gewürzen und Wasser im Modell nicht berücksichtigt werden, da diese Zutaten ja sowieso in unbegrenzter Kapazität zur Verfügung stehen. Ich habe dies auch mit einem Simplexrechner überprüft, indem ich diese Restriktionen mit extrem großen Zahlen berücksichtigt habe und habe damit das gleiche Ergebnis wie oben erhalten.
LG Lisa
bei Aufgabe 2 habe ich die gleichen Ergebnisse wie du. Bei Aufgabe 1 habe ich die Lösung (x1,x2,x3,x4,x5,x6)^T=(0,0,5,135,195,35)^T mit x0=10 erhalten. Wie sieht dein Optimierungsmodell aus? Ich habe mit folgendem gerechnet:
Max x0=1,5x1+2,5x2+2x3
u.d.N.
x1+1,5x2+x3<=5
x1+x3<=140
2x2+x3<=200
x1+x2+x3<=40
x1,x2,x3>=0
M.E. müssen die Restriktionen zu Hefe, Gewürzen und Wasser im Modell nicht berücksichtigt werden, da diese Zutaten ja sowieso in unbegrenzter Kapazität zur Verfügung stehen. Ich habe dies auch mit einem Simplexrechner überprüft, indem ich diese Restriktionen mit extrem großen Zahlen berücksichtigt habe und habe damit das gleiche Ergebnis wie oben erhalten.
LG Lisa
Hallo Lisa,
laut Angabe hat der Backofen 40 Plätze.
Statt 5h einen Ofen mit 40 Plätzen zu benutzen, hab ich 40*5h=200h einen Ofen mit nur einem Backplatz modelliert.
Die 1. Nebenbedingung lautet dann bei mir: x1+1,5x2+x3<=200.
Deine letzte Nebenbedingung (x1+x2+x3<=40) passt nicht.
Das würde bedeuten, dass Du insgesamt maximal 40 Brote machen kannst.
Man darf aber die Plätze im Ofen (nachdem das aktuelle Brot fertig gebacken ist) wieder verwenden.
Ich habe nur 3 Nebenbedingen:
Die obige 1. Nebenbedingung und Deine 2. und 3. Nebenbedingung (Weizenmehl, Roggenmehl).
Bei Aufgabenteil d) musst Du dann aufpassen.
Das berechnete Zeitintervall bezieht sich bei meiner Modellierung auf den "1-Platz"-Ofen.
Entsprechend musst Du die berechnete Zeit durch 40 teilen, um auf den 40-Platz-Ofen zu kommen.
LG Andreas
laut Angabe hat der Backofen 40 Plätze.
Statt 5h einen Ofen mit 40 Plätzen zu benutzen, hab ich 40*5h=200h einen Ofen mit nur einem Backplatz modelliert.
Die 1. Nebenbedingung lautet dann bei mir: x1+1,5x2+x3<=200.
Deine letzte Nebenbedingung (x1+x2+x3<=40) passt nicht.
Das würde bedeuten, dass Du insgesamt maximal 40 Brote machen kannst.
Man darf aber die Plätze im Ofen (nachdem das aktuelle Brot fertig gebacken ist) wieder verwenden.
Ich habe nur 3 Nebenbedingen:
Die obige 1. Nebenbedingung und Deine 2. und 3. Nebenbedingung (Weizenmehl, Roggenmehl).
Bei Aufgabenteil d) musst Du dann aufpassen.
Das berechnete Zeitintervall bezieht sich bei meiner Modellierung auf den "1-Platz"-Ofen.
Entsprechend musst Du die berechnete Zeit durch 40 teilen, um auf den 40-Platz-Ofen zu kommen.
LG Andreas
Hallo Andreas,
ich habe den das Modell nochmals berechnet und erhalte die gleichen Ergebnisse wie du mit x0=370. Deine Ausführungen zu d) kann ich nicht ganz nachvollziehen. Die Inverse lautet:
4/3 -1/3 -1
-4/3 4/3 1
2/3 -2/3 0
Wenn ich im Anschluss v=(1,0,0)^T verwende, erhalte ich andere Werte als du.
LG Lisa
ich habe den das Modell nochmals berechnet und erhalte die gleichen Ergebnisse wie du mit x0=370. Deine Ausführungen zu d) kann ich nicht ganz nachvollziehen. Die Inverse lautet:
4/3 -1/3 -1
-4/3 4/3 1
2/3 -2/3 0
Wenn ich im Anschluss v=(1,0,0)^T verwende, erhalte ich andere Werte als du.
LG Lisa
Hallo Lisa,
im Prinzip habe ich die gleichen Inverse.
(Die letzten beiden Zeilen hab ich getauscht. Das sollte aber nichts an der Sensitivitätsanalyse verändern.)
Was hast Du für b(Tilde) und v(Tilde) rausbekommen (siehe KE3, S2)?
Bei mir ist b(Tilde)= (20 40 120)^T und v(Tilde) = (4/3, 2/3, -4/3)^T.
Ich glaube, dass ich danach einen Fehler in der Rechnung habe.
Vielleicht ist auch das Intervall [4.575h und 7.25h] richtig.
Das muss ich mir am Wochenende mal genauer ansehen.
LG
Andreas
im Prinzip habe ich die gleichen Inverse.
(Die letzten beiden Zeilen hab ich getauscht. Das sollte aber nichts an der Sensitivitätsanalyse verändern.)
Was hast Du für b(Tilde) und v(Tilde) rausbekommen (siehe KE3, S2)?
Bei mir ist b(Tilde)= (20 40 120)^T und v(Tilde) = (4/3, 2/3, -4/3)^T.
Ich glaube, dass ich danach einen Fehler in der Rechnung habe.
Vielleicht ist auch das Intervall [4.575h und 7.25h] richtig.
Das muss ich mir am Wochenende mal genauer ansehen.
LG
Andreas
Hallo Lisa,
ja genau.... dann hat man beim "1-Platz-Ofen-Modell" das Zeitintervall [200-15 ; 200+90]=[185h, 290h].
Und wenn Du auf das "40-Plätze-Ofen-Modell" zurückgeht, musst Du die Werte wieder durch 40 teilen.
Dann ist man bei [4.625h; 7.25h]. Das müsste dann die richtige Lösung sein (denke ich....).
LG Andreas
ja genau.... dann hat man beim "1-Platz-Ofen-Modell" das Zeitintervall [200-15 ; 200+90]=[185h, 290h].
Und wenn Du auf das "40-Plätze-Ofen-Modell" zurückgeht, musst Du die Werte wieder durch 40 teilen.
Dann ist man bei [4.625h; 7.25h]. Das müsste dann die richtige Lösung sein (denke ich....).
LG Andreas
Hallo Lisa,
das Intervall, das bei d2 gefragt ist, sind die [-15;90] =[l_min;l_max].
Ich war schon bei der d3:
Bei d3 habe ich durch 40 geteilt und auf die Backzeit (plus 5h) umgerechnet.
=> Liegt die "Backzeit" im Bereich zwischen 4.625h und 7.25h, so ist die gefundene Basis optimal.
Das muss man aber nicht so machen.
Man könnte auch sagen, falls die Backzeit um 2.25h verlängert oder um 0.375h (noch besser 22.5 min) verkürzt wird,
ist die gefundene Basis optimal.
Das ist nur "Kosmetik"
Viele Grüße
Andreas
das Intervall, das bei d2 gefragt ist, sind die [-15;90] =[l_min;l_max].
Ich war schon bei der d3:
Bei d3 habe ich durch 40 geteilt und auf die Backzeit (plus 5h) umgerechnet.
=> Liegt die "Backzeit" im Bereich zwischen 4.625h und 7.25h, so ist die gefundene Basis optimal.
Das muss man aber nicht so machen.
Man könnte auch sagen, falls die Backzeit um 2.25h verlängert oder um 0.375h (noch besser 22.5 min) verkürzt wird,
ist die gefundene Basis optimal.
Das ist nur "Kosmetik"
Viele Grüße
Andreas
Hallo zusammen,
ich zeichne gerade zu Aufgabe 2b).
Ist es richtig, dass die Zielfunktion durch den 0-Punkt geht?
LG Anne
ich zeichne gerade zu Aufgabe 2b).
Ist es richtig, dass die Zielfunktion durch den 0-Punkt geht?
LG Anne
Hallo Anne,
die Zielfunktion kannst Du durch den Ursprung zeichnen.
Der Zielfunktionswert wäre dann zwar 0, aber die Gerade liegt dann aber nicht mehr im zulässigen Bereich.
Daher wäre diese Gerade nicht zulässig.
Wenn Du die Zielfunktion ein wenig nach rechts verschiebst, damit zumindest ein Punkt der Geraden im zulässigen Bereich liegt,
erreichst Du den (minimalen) Zielfunktionswert 27.
Hinweis: Die Gerade geht dann durch den Punkt (3,3), der auch im zulässigen Bereich liegt.
Viele Grüße
Andreas
die Zielfunktion kannst Du durch den Ursprung zeichnen.
Der Zielfunktionswert wäre dann zwar 0, aber die Gerade liegt dann aber nicht mehr im zulässigen Bereich.
Daher wäre diese Gerade nicht zulässig.
Wenn Du die Zielfunktion ein wenig nach rechts verschiebst, damit zumindest ein Punkt der Geraden im zulässigen Bereich liegt,
erreichst Du den (minimalen) Zielfunktionswert 27.
Hinweis: Die Gerade geht dann durch den Punkt (3,3), der auch im zulässigen Bereich liegt.
Viele Grüße
Andreas
Könnt ihr mir einmal auf die Sprünge helfen ;)
In Aufgabe 1c steht "Überführen sie das primale LOP in das äquivalente Maximierungsproblem". Ist das nicht das duale LOP aus Aufgabe 1a?
Sorry für die komischen Fragen, aber ich hab noch ein Brett vor dem Kopf.
In Aufgabe 1c steht "Überführen sie das primale LOP in das äquivalente Maximierungsproblem". Ist das nicht das duale LOP aus Aufgabe 1a?
Sorry für die komischen Fragen, aber ich hab noch ein Brett vor dem Kopf.
Hallo Anne,
ich gehe davon aus, dass Du Aufgabe 2a und 2c meinst, oder?
Bei Aufgabe 2a gehst Du in Prinzip wie in Übungsaufgabe 5.1 iii) aus KE2 vor.
Statt den "x"-Variablen, hast Du dann "u"-Variablen.
Aus Spalten werden Zeilen und umgekeht ("Transponieren")
Bei Aufgabe 2c gehst Du wie in Übungsaufgabe 3.3 aus KE1 vor.
Hier bleibt es bei den "x"-Variablen.
Im Prinzip multiplizierst Du Zeilen mit "-1"
Viele Grüße
Andreas
ich gehe davon aus, dass Du Aufgabe 2a und 2c meinst, oder?
Bei Aufgabe 2a gehst Du in Prinzip wie in Übungsaufgabe 5.1 iii) aus KE2 vor.
Statt den "x"-Variablen, hast Du dann "u"-Variablen.
Aus Spalten werden Zeilen und umgekeht ("Transponieren")
Bei Aufgabe 2c gehst Du wie in Übungsaufgabe 3.3 aus KE1 vor.
Hier bleibt es bei den "x"-Variablen.
Im Prinzip multiplizierst Du Zeilen mit "-1"
Viele Grüße
Andreas
Anhänge
Hallo Anna,
zur Übungsaufgabe 3.3 aus dem Skript:
Die 1. ursprüngliche NB ist "kleiner gleich", die 2. urspüngliche NB ist "größer gleich".
Das ist der Grund für "die positive und die negative Schlupfvariable".
Nach "Einführung der Schlupfvariablen" werden die Ungleichungen zu Gleichungen.
Bei 2a und 2b habe ich die gleiche Lösung wie Du.
Deine Schlupfvariablen bei Aufabe 2c haben (meiner Meinung nach) das falsche Vorzeichen.
Wenn z.B. x1+x2 >=5 (4+3 = 7 >=5) dann folgt daraus x1 + x2 - s = 5 (also 4+3 - 2 = 5).
Die Schlupfvariable nimmt den Anteil, der über 5 liegt, auf.
Da die Schlupfvariable selbst per Definition positiv ist (z.B. +2), muss der Koeffizient davor "-1" sein.
Deine Zeichnung bei Aufgabe 2b hab ich genauso
Viele Grüße
Andreas
zur Übungsaufgabe 3.3 aus dem Skript:
Die 1. ursprüngliche NB ist "kleiner gleich", die 2. urspüngliche NB ist "größer gleich".
Das ist der Grund für "die positive und die negative Schlupfvariable".
Nach "Einführung der Schlupfvariablen" werden die Ungleichungen zu Gleichungen.
Bei 2a und 2b habe ich die gleiche Lösung wie Du.
Deine Schlupfvariablen bei Aufabe 2c haben (meiner Meinung nach) das falsche Vorzeichen.
Wenn z.B. x1+x2 >=5 (4+3 = 7 >=5) dann folgt daraus x1 + x2 - s = 5 (also 4+3 - 2 = 5).
Die Schlupfvariable nimmt den Anteil, der über 5 liegt, auf.
Da die Schlupfvariable selbst per Definition positiv ist (z.B. +2), muss der Koeffizient davor "-1" sein.
Deine Zeichnung bei Aufgabe 2b hab ich genauso
Viele Grüße
Andreas
Okay, dann habe ich verstanden:
>=, dann Schlupfvariable negativ
<=, dann Schlupfvariable positiv
Ich habe nochmal eine Frage zur Aufgabenstellung. Da tue ich mich recht schwer.
Aufgabe c)
"Geben Sie ausgehend von der Berechnung jeweils für das primale und das zugehörige duale LOP die optimale Lösung einschließlich ZFW an."
Für das primale LOP habe ich doch bereits in 2a) die optimale Lösung ermittelt. Oder ist jetzt mein überführtes Maximierungsproblem das primale LOP?
Andreas, du hattest oben auch nur eine Lösung angegeben. Ist das der Grund?
>=, dann Schlupfvariable negativ
<=, dann Schlupfvariable positiv
Ich habe nochmal eine Frage zur Aufgabenstellung. Da tue ich mich recht schwer.
Aufgabe c)
"Geben Sie ausgehend von der Berechnung jeweils für das primale und das zugehörige duale LOP die optimale Lösung einschließlich ZFW an."
Für das primale LOP habe ich doch bereits in 2a) die optimale Lösung ermittelt. Oder ist jetzt mein überführtes Maximierungsproblem das primale LOP?
Andreas, du hattest oben auch nur eine Lösung angegeben. Ist das der Grund?