App installieren
So wird die App in iOS installiert
Folge dem Video um zu sehen, wie unsere Website als Web-App auf dem Startbildschirm installiert werden kann.
Anmerkung: Diese Funktion ist in einigen Browsern möglicherweise nicht verfügbar.
- Wirtschaft
- Bachelor Wirtschaftswissenschaft
- Pflichtmodule Bachelor WiWi
- 31021 Investition und Finanzierung (BWL II)
Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Ich :)Wäre jemand an einer Whatsappgruppe interessiert?
Ich auch :) gerne auch zu int/ext Rechnungswesen, ich trete dieses Semester zur Triade an.Ich :)
G
GelöschterUser4789
abgemeldet
Wäre jemand an einer Whatsappgruppe interessiert?
Ich hätte auch Interesse
Super Idee. Ich habe den Finanzierungsteil begonnen und Aufgabe 1 komplett gelöst und von Aufgabe 2 das Meiste. Bin jedoch sehr unsicher, ob es stimmt.Hallo zusammen, würde mich auch gerne bzgl. der EA austauschen. Sollen wir hierzu einen eigenen Thread erstellen?
Mal mein Gedankengut zu Finanzierung. Das Skript finde ich teilweise nicht gerade hilfreich. Bitte nicht blind kopieren!
Aufgabe 1)
a)
siehe §192 Abs. 2 Nr. 1 bis 3 AktG
b)
In diesem Fall §192 Abs. 2 Nr. 1 AktG
d)
Geg.:
Bilanzielles Eigenkapital (laut Jahresabschluss) = 2.924.440.000 €
Anzahl Aktien (laut Aufgabenstellung) = 590.415.100
Ges.:
Bilanzkurs = Bilanzielles Eigenkapital / Anzahl Aktien
= 2.924.440.000 € / 590.415.100
= 4,95 €
Aufgabe 2)
a)
Bei einem Kapitalschnitt wird eine Kapitalherabsetzung mit anschließender Kapitalerhöhung vorgenommen. Dabei wird das gezeichnete Kapital reduziert, so dass eine anschließende Kapitalerhöhung für neue Kapitalgeber attraktiv wird. Vergangene Verluste werden im gezeichneten Kapital sichtbar, sie werden also in dieser Bilanzposition den Altaktionären zugeschrieben. Dadurch wird der Weg für neue Aktionäre frei.
b)
Eigenkapital_Schnitt = Eigenkapital_30.09.2020 = 2.924.440 T€
Gezeichnetes Kapital_Schnitt = Gezeichnetes Kapital_30.09.2020 / 2,56 € * 1 €
= 1.509.372 T€ / 2,56 € * 1 €
= 589.598 T€
Bilanzgewinn_Schnitt = Bilanzgewinn_30.09.2020 = 190.874 T€
Kapitalrücklage_Schnitt = Eigenkapital_neu – Gezeichnetes Kapital_neu – Bilanzgewinn_neu
= 2.924.440 T€ – 589.598 T€ – 190.874 T€
= 2.143.968 T€
c)
Nominalvolumen = 508.978.534 €
Bezugskurs A = 1,07 €
Bezugsverhältnis b = n_alt / n_jung = 29 : 25
d)
Zweck der Maßnahme ist die nominelle Reduzierung des Grundkapitals, so dass eine anschließende Kapitalerhöhung für neue Kapitalgeber attraktiv wird. Die in der Vergangenheit aufgetretenen Verluste werden so im gezeichneten Kapital sichtbar, sie werden also in dieser Bilanzposition den Altaktionären zugeschrieben. Durch diese auch im Grundkapital sichtbar gewordene Verlustübernahme seitens der Altaktionäre wird gesetzlich wie ökonomisch der Weg für die Aufnahme neuer Aktionäre frei.
e)
Geg.:
b = n_alt / n_jung = 29 / 25 = 1,16
K_alt = 5,48 €
A = 1,07 €
Ges.:
B = ( K_alt – A ) / ( 1 + b ) = ( 5,48 € – 1,07 €) / ( 1 + 1,16 ) = 2,04 €
f)
Geg.:
A = 1,07 €
B = 2,04 €
K_alt = 5,48 €
n_alt = 590.415.100
n_jung = 508.978.534
Ges.:
K_neu
kurz:
K_alt = K_neu + B
K_neu = K_alt – B = 5,48 € – 2,04 € = 3,44 €
lang:
K_neu = ( n_alt * K_alt + n_jung * A ) / ( n_alt + n_jung )
= ( n_alt * K_alt + n_jung * A ) / 1.099.393.634
= ( 590.415.100 * 5,48 € + 508.978.534 * 1.07 € ) / 1.099.393.634
= 3,44 €
g)
Geg.:
Nominalvolumen = 508.978.534 € = 508.979 T€
Gezeichnetes Kapital_Schnitt = 589.598 T€
Kapitalrücklage_Schnitt = 2.143.968 T€
Ges.:
Gezeichnetes Kapital_neu = Gezeichnetes Kapital_Schnitt + Nominalvolumen
= 589.598 T€ + 508.979 T€
= 1.098.577 T€
Kapitalrücklage_neu = Kapitalrücklage_Schnitt = 2.143.968 T€
Aufgabe 3)
a)
Geg.:
K_real = 4,21 €
K_neu = 3,44 € (aus 2f)
B_real = 2,48 €
B = 2,04 € (aus 2e)
Ges.:
K_real – K_neu = 4,21 € – 3,44 € = 0,77 €
B_real – B = 2,48 € – 2,04 € = 0,34 €
Aktie und Bezugsrecht sind real mehr wert als der jeweils errechnete theoretische Wert.
b)
Geg.:
#Aktien_alt = 5.800
K_alt = 5,48 € (aus 2e)
K_real = 4,21 € (aus 3a)
B_real = 2,48 € (aus 3a)
Ges.:
Vermögen_alt = #Aktien_alt * K_alt = 5.800 * 5,48 € = 31.784 €
Vermögen_neu = #Aktien_alt * ( K_real + B_real ) = 5.800 * ( 4,21 € + 2,48 € ) = 38.802 €
Vermögen_neu – Vermögen_alt = 38.802 € – 31.784 € = 7.018 €
Der Aktionär hat einen Vermögenszuwachs von 7.018 €.
c)
Geg.:
#Aktien_alt = 5.800
K_real = 4,21 € (aus 3a)
Vermögen_alt = 31.784 € (aus 3b)
A = 1,07 € (aus 2c)
#Aktien_neu = 5.000 (aus 3b)
Ges.:
Vermögen_neu = #Aktien_alt * K_real + #Aktien_neu * ( K_real – A )
= 5.800 * 4,21 € + 5.000 * ( 4,21 € – 1,07 € )
= 24.418 € + 15.700 €
= 40.118 €
Vermögen_neu – Vermögen_alt = 40.118 € – 31.784 € = 8.334 €
Der Aktionär hat einen Vermögenszuwachs von 8.334 €.
d)
Geg.:
#Aktien_alt = 5.800 (aus 3b)
K_real = 4,21 € (aus 3a)
A = 1,07 € (aus 2c)
B_real = 2,48 € (aus 3a)
n_alt = 29 (aus 2c)
n_jung = 25 (aus 2c)
b = n_alt / n_jung = 29 / 25 = 1,16 (aus 2e)
Vermögen_alt = 31.784 € (aus 3b)
#B = #Aktien_alt
Ges.:
#B_verkauf = ( #Aktien_alt * n_jung * A ) / ( n_jung * A + n_alt * B_real )
= ( 5.800 * 25 * 1,07 € ) / ( 25 * 1,07 € + 29 * 2,48 € )
= 155.150 € / 98,67 €
= 1.572,413094
≈ 1.573
#Aktien_jung = ( #B * B_real ) / ( A + B_real * b )
= ( 5.800 * 2,48 € ) / ( 1,07 € + 2,48 € * 1,16 )
= 14.384 € / 3,9468 €
= 3644,471471
≈ 3644
Verkaufserlös Bezugsrechte: 1.573 * 2,48 € = 3.901,04 €
Bezugspreis neue Aktien: 3.644 * 1,07 € = 3.899,08 €
Überschuss: 3.901,04 € – 3.899,08 € = 1,96 €
Vermögen_neu = ( #Aktien_alt + #Aktien_jung ) * K_real
= ( 5.800 + 3.644 ) * 4,21 €
= 9.444 * 4,21 €
= 39.759,24 €
Vermögen_neu – Vermögen_alt = 39.759,24 € – 31.784 € = 7.975,24 €
Der Aktionär hat einen Vermögenszuwachs von 7.975,24 € plus 1,96 € Überschuss.
Aufgabe 1)
a)
siehe §192 Abs. 2 Nr. 1 bis 3 AktG
b)
In diesem Fall §192 Abs. 2 Nr. 1 AktG
d)
Geg.:
Bilanzielles Eigenkapital (laut Jahresabschluss) = 2.924.440.000 €
Anzahl Aktien (laut Aufgabenstellung) = 590.415.100
Ges.:
Bilanzkurs = Bilanzielles Eigenkapital / Anzahl Aktien
= 2.924.440.000 € / 590.415.100
= 4,95 €
Aufgabe 2)
a)
Bei einem Kapitalschnitt wird eine Kapitalherabsetzung mit anschließender Kapitalerhöhung vorgenommen. Dabei wird das gezeichnete Kapital reduziert, so dass eine anschließende Kapitalerhöhung für neue Kapitalgeber attraktiv wird. Vergangene Verluste werden im gezeichneten Kapital sichtbar, sie werden also in dieser Bilanzposition den Altaktionären zugeschrieben. Dadurch wird der Weg für neue Aktionäre frei.
b)
Eigenkapital_Schnitt = Eigenkapital_30.09.2020 = 2.924.440 T€
Gezeichnetes Kapital_Schnitt = Gezeichnetes Kapital_30.09.2020 / 2,56 € * 1 €
= 1.509.372 T€ / 2,56 € * 1 €
= 589.598 T€
Bilanzgewinn_Schnitt = Bilanzgewinn_30.09.2020 = 190.874 T€
Kapitalrücklage_Schnitt = Eigenkapital_neu – Gezeichnetes Kapital_neu – Bilanzgewinn_neu
= 2.924.440 T€ – 589.598 T€ – 190.874 T€
= 2.143.968 T€
c)
Nominalvolumen = 508.978.534 €
Bezugskurs A = 1,07 €
Bezugsverhältnis b = n_alt / n_jung = 29 : 25
d)
Zweck der Maßnahme ist die nominelle Reduzierung des Grundkapitals, so dass eine anschließende Kapitalerhöhung für neue Kapitalgeber attraktiv wird. Die in der Vergangenheit aufgetretenen Verluste werden so im gezeichneten Kapital sichtbar, sie werden also in dieser Bilanzposition den Altaktionären zugeschrieben. Durch diese auch im Grundkapital sichtbar gewordene Verlustübernahme seitens der Altaktionäre wird gesetzlich wie ökonomisch der Weg für die Aufnahme neuer Aktionäre frei.
e)
Geg.:
b = n_alt / n_jung = 29 / 25 = 1,16
K_alt = 5,48 €
A = 1,07 €
Ges.:
B = ( K_alt – A ) / ( 1 + b ) = ( 5,48 € – 1,07 €) / ( 1 + 1,16 ) = 2,04 €
f)
Geg.:
A = 1,07 €
B = 2,04 €
K_alt = 5,48 €
n_alt = 590.415.100
n_jung = 508.978.534
Ges.:
K_neu
kurz:
K_alt = K_neu + B
K_neu = K_alt – B = 5,48 € – 2,04 € = 3,44 €
lang:
K_neu = ( n_alt * K_alt + n_jung * A ) / ( n_alt + n_jung )
= ( n_alt * K_alt + n_jung * A ) / 1.099.393.634
= ( 590.415.100 * 5,48 € + 508.978.534 * 1.07 € ) / 1.099.393.634
= 3,44 €
g)
Geg.:
Nominalvolumen = 508.978.534 € = 508.979 T€
Gezeichnetes Kapital_Schnitt = 589.598 T€
Kapitalrücklage_Schnitt = 2.143.968 T€
Ges.:
Gezeichnetes Kapital_neu = Gezeichnetes Kapital_Schnitt + Nominalvolumen
= 589.598 T€ + 508.979 T€
= 1.098.577 T€
Kapitalrücklage_neu = Kapitalrücklage_Schnitt = 2.143.968 T€
Aufgabe 3)
a)
Geg.:
K_real = 4,21 €
K_neu = 3,44 € (aus 2f)
B_real = 2,48 €
B = 2,04 € (aus 2e)
Ges.:
K_real – K_neu = 4,21 € – 3,44 € = 0,77 €
B_real – B = 2,48 € – 2,04 € = 0,34 €
Aktie und Bezugsrecht sind real mehr wert als der jeweils errechnete theoretische Wert.
b)
Geg.:
#Aktien_alt = 5.800
K_alt = 5,48 € (aus 2e)
K_real = 4,21 € (aus 3a)
B_real = 2,48 € (aus 3a)
Ges.:
Vermögen_alt = #Aktien_alt * K_alt = 5.800 * 5,48 € = 31.784 €
Vermögen_neu = #Aktien_alt * ( K_real + B_real ) = 5.800 * ( 4,21 € + 2,48 € ) = 38.802 €
Vermögen_neu – Vermögen_alt = 38.802 € – 31.784 € = 7.018 €
Der Aktionär hat einen Vermögenszuwachs von 7.018 €.
c)
Geg.:
#Aktien_alt = 5.800
K_real = 4,21 € (aus 3a)
Vermögen_alt = 31.784 € (aus 3b)
A = 1,07 € (aus 2c)
#Aktien_neu = 5.000 (aus 3b)
Ges.:
Vermögen_neu = #Aktien_alt * K_real + #Aktien_neu * ( K_real – A )
= 5.800 * 4,21 € + 5.000 * ( 4,21 € – 1,07 € )
= 24.418 € + 15.700 €
= 40.118 €
Vermögen_neu – Vermögen_alt = 40.118 € – 31.784 € = 8.334 €
Der Aktionär hat einen Vermögenszuwachs von 8.334 €.
d)
Geg.:
#Aktien_alt = 5.800 (aus 3b)
K_real = 4,21 € (aus 3a)
A = 1,07 € (aus 2c)
B_real = 2,48 € (aus 3a)
n_alt = 29 (aus 2c)
n_jung = 25 (aus 2c)
b = n_alt / n_jung = 29 / 25 = 1,16 (aus 2e)
Vermögen_alt = 31.784 € (aus 3b)
#B = #Aktien_alt
Ges.:
#B_verkauf = ( #Aktien_alt * n_jung * A ) / ( n_jung * A + n_alt * B_real )
= ( 5.800 * 25 * 1,07 € ) / ( 25 * 1,07 € + 29 * 2,48 € )
= 155.150 € / 98,67 €
= 1.572,413094
≈ 1.573
#Aktien_jung = ( #B * B_real ) / ( A + B_real * b )
= ( 5.800 * 2,48 € ) / ( 1,07 € + 2,48 € * 1,16 )
= 14.384 € / 3,9468 €
= 3644,471471
≈ 3644
Verkaufserlös Bezugsrechte: 1.573 * 2,48 € = 3.901,04 €
Bezugspreis neue Aktien: 3.644 * 1,07 € = 3.899,08 €
Überschuss: 3.901,04 € – 3.899,08 € = 1,96 €
Vermögen_neu = ( #Aktien_alt + #Aktien_jung ) * K_real
= ( 5.800 + 3.644 ) * 4,21 €
= 9.444 * 4,21 €
= 39.759,24 €
Vermögen_neu – Vermögen_alt = 39.759,24 € – 31.784 € = 7.975,24 €
Der Aktionär hat einen Vermögenszuwachs von 7.975,24 € plus 1,96 € Überschuss.
Hallo Erdi,Mal mein Gedankengut zu Finanzierung. Das Skript finde ich teilweise nicht gerade hilfreich. Bitte nicht blind kopieren!
Aufgabe 1)
a)
siehe §192 Abs. 2 Nr. 1 bis 3 AktG
b)
In diesem Fall §192 Abs. 2 Nr. 1 AktG
d)
Geg.:
Bilanzielles Eigenkapital (laut Jahresabschluss) = 2.924.440.000 €
Anzahl Aktien (laut Aufgabenstellung) = 590.415.100
Ges.:
Bilanzkurs = Bilanzielles Eigenkapital / Anzahl Aktien
= 2.924.440.000 € / 590.415.100
= 4,95 €
Aufgabe 2)
a)
Bei einem Kapitalschnitt wird eine Kapitalherabsetzung mit anschließender Kapitalerhöhung vorgenommen. Dabei wird das gezeichnete Kapital reduziert, so dass eine anschließende Kapitalerhöhung für neue Kapitalgeber attraktiv wird. Vergangene Verluste werden im gezeichneten Kapital sichtbar, sie werden also in dieser Bilanzposition den Altaktionären zugeschrieben. Dadurch wird der Weg für neue Aktionäre frei.
b)
Eigenkapital_Schnitt = Eigenkapital_30.09.2020 = 2.924.440 T€
Gezeichnetes Kapital_Schnitt = Gezeichnetes Kapital_30.09.2020 / 2,56 € * 1 €
= 1.509.372 T€ / 2,56 € * 1 €
= 589.598 T€
Bilanzgewinn_Schnitt = Bilanzgewinn_30.09.2020 = 190.874 T€
Kapitalrücklage_Schnitt = Eigenkapital_neu – Gezeichnetes Kapital_neu – Bilanzgewinn_neu
= 2.924.440 T€ – 589.598 T€ – 190.874 T€
= 2.143.968 T€
c)
Nominalvolumen = 508.978.534 €
Bezugskurs A = 1,07 €
Bezugsverhältnis b = n_alt / n_jung = 29 : 25
d)
Zweck der Maßnahme ist die nominelle Reduzierung des Grundkapitals, so dass eine anschließende Kapitalerhöhung für neue Kapitalgeber attraktiv wird. Die in der Vergangenheit aufgetretenen Verluste werden so im gezeichneten Kapital sichtbar, sie werden also in dieser Bilanzposition den Altaktionären zugeschrieben. Durch diese auch im Grundkapital sichtbar gewordene Verlustübernahme seitens der Altaktionäre wird gesetzlich wie ökonomisch der Weg für die Aufnahme neuer Aktionäre frei.
e)
Geg.:
b = n_alt / n_jung = 29 / 25 = 1,16
K_alt = 5,48 €
A = 1,07 €
Ges.:
B = ( K_alt – A ) / ( 1 + b ) = ( 5,48 € – 1,07 €) / ( 1 + 1,16 ) = 2,04 €
f)
Geg.:
A = 1,07 €
B = 2,04 €
K_alt = 5,48 €
n_alt = 590.415.100
n_jung = 508.978.534
Ges.:
K_neu
kurz:
K_alt = K_neu + B
K_neu = K_alt – B = 5,48 € – 2,04 € = 3,44 €
lang:
K_neu = ( n_alt * K_alt + n_jung * A ) / ( n_alt + n_jung )
= ( n_alt * K_alt + n_jung * A ) / 1.099.393.634
= ( 590.415.100 * 5,48 € + 508.978.534 * 1.07 € ) / 1.099.393.634
= 3,44 €
g)
Geg.:
Nominalvolumen = 508.978.534 € = 508.979 T€
Gezeichnetes Kapital_Schnitt = 589.598 T€
Kapitalrücklage_Schnitt = 2.143.968 T€
Ges.:
Gezeichnetes Kapital_neu = Gezeichnetes Kapital_Schnitt + Nominalvolumen
= 589.598 T€ + 508.979 T€
= 1.098.577 T€
Kapitalrücklage_neu = Kapitalrücklage_Schnitt = 2.143.968 T€
Aufgabe 3)
a)
Geg.:
K_real = 4,21 €
K_neu = 3,44 € (aus 2f)
B_real = 2,48 €
B = 2,04 € (aus 2e)
Ges.:
K_real – K_neu = 4,21 € – 3,44 € = 0,77 €
B_real – B = 2,48 € – 2,04 € = 0,34 €
Aktie und Bezugsrecht sind real mehr wert als der jeweils errechnete theoretische Wert.
b)
Geg.:
#Aktien_alt = 5.800
K_alt = 5,48 € (aus 2e)
K_real = 4,21 € (aus 3a)
B_real = 2,48 € (aus 3a)
Ges.:
Vermögen_alt = #Aktien_alt * K_alt = 5.800 * 5,48 € = 31.784 €
Vermögen_neu = #Aktien_alt * ( K_real + B_real ) = 5.800 * ( 4,21 € + 2,48 € ) = 38.802 €
Vermögen_neu – Vermögen_alt = 38.802 € – 31.784 € = 7.018 €
Der Aktionär hat einen Vermögenszuwachs von 7.018 €.
c)
Geg.:
#Aktien_alt = 5.800
K_real = 4,21 € (aus 3a)
Vermögen_alt = 31.784 € (aus 3b)
A = 1,07 € (aus 2c)
#Aktien_neu = 5.000 (aus 3b)
Ges.:
Vermögen_neu = #Aktien_alt * K_real + #Aktien_neu * ( K_real – A )
= 5.800 * 4,21 € + 5.000 * ( 4,21 € – 1,07 € )
= 24.418 € + 15.700 €
= 40.118 €
Vermögen_neu – Vermögen_alt = 40.118 € – 31.784 € = 8.334 €
Der Aktionär hat einen Vermögenszuwachs von 8.334 €.
d)
Geg.:
#Aktien_alt = 5.800 (aus 3b)
K_real = 4,21 € (aus 3a)
A = 1,07 € (aus 2c)
B_real = 2,48 € (aus 3a)
n_alt = 29 (aus 2c)
n_jung = 25 (aus 2c)
b = n_alt / n_jung = 29 / 25 = 1,16 (aus 2e)
Vermögen_alt = 31.784 € (aus 3b)
#B = #Aktien_alt
Ges.:
#B_verkauf = ( #Aktien_alt * n_jung * A ) / ( n_jung * A + n_alt * B_real )
= ( 5.800 * 25 * 1,07 € ) / ( 25 * 1,07 € + 29 * 2,48 € )
= 155.150 € / 98,67 €
= 1.572,413094
≈ 1.573
#Aktien_jung = ( #B * B_real ) / ( A + B_real * b )
= ( 5.800 * 2,48 € ) / ( 1,07 € + 2,48 € * 1,16 )
= 14.384 € / 3,9468 €
= 3644,471471
≈ 3644
Verkaufserlös Bezugsrechte: 1.573 * 2,48 € = 3.901,04 €
Bezugspreis neue Aktien: 3.644 * 1,07 € = 3.899,08 €
Überschuss: 3.901,04 € – 3.899,08 € = 1,96 €
Vermögen_neu = ( #Aktien_alt + #Aktien_jung ) * K_real
= ( 5.800 + 3.644 ) * 4,21 €
= 9.444 * 4,21 €
= 39.759,24 €
Vermögen_neu – Vermögen_alt = 39.759,24 € – 31.784 € = 7.975,24 €
Der Aktionär hat einen Vermögenszuwachs von 7.975,24 € plus 1,96 € Überschuss.
Aufgaben 1 und 2 a-e habe ich genauso.
Bei 2 g habe ich andere Ergebnisse:
Gezeichnetes Kapital: 1.099.394 t€
Kapitalrücklage: 2.143.151 t€
Bilanzgewinn: 190.874 t€
Gesamt: 3.433.419 t€
Bei 3 a habe ich bisher gar nichts.
3 b und c habe ich komplett anders, aber ich habe auch wirklich keine Ahnung und die Aufgaben nur nach Gefühl gelöst.
3 b)
5800 Alt-Aktien entsprechen zu Handelsbeginn am 8.1. -> 5.800 * 4,21 = 24.418 € Vermögen
Sein Bezugsrecht ist: 29 alt : 25 neu -> 5.800 *25/29 = 5.000
Bezugsrecht ausgeübt: 5.000 * 1,07 = 5.350 € Aufwand
Bezugsrechte zu Handelsbeginn verkauft: 5.000 * 4,21 = 21.050 Ertrag - 5.350 Aufwand = 15.700 €
Zu seinem Altvermögen in Höhe von 24.418 € kommen 15.700 € Vermögen dazu.
3 c)
Vermögen Handelsbeginn Altaktien: 24.418 €
Bezugsrecht ausgeübt: 5.350 € Aufwand
Aktien gesamt: 10.800
Börsenschluss: 10.800 * 2,48 € = 26.784 € Vermögen
26.784 € - 24.418 € - 5.350 € = - 2.984 €
Seine Vermögenspostition verschlechtert sich um 2.984 €.
3 d habe ich auch so gelöst, allerdings habe ich die Rechnung auch noch einmal mit dem Eröffnungskurs von 4,21 € gemacht.
Hast Du Investition schon gelöst?
An Investition sitze ich gerade dran. Hoffentlich kriege ich das heute fertig.
Zu 2g)
Der Unterschied dürfte durch die Art der Berechnung entstehen. Ich hab mit dem Wert von oben weitergerechnet. Da haben ich gez. Kapital durch die 2,56 € geteilt. Du hast vermutlich einfach die Anzahl der alten und neuen Aktien zusammengenommen und mit 1€ multipliziert.
Zu 3b/c/d)
Du vermischt hier ein paar Dinge. Bezugsrechte beziehen sich auf die Altaktien. Pro alter Aktie hat er ein Bezugsrecht. Aber zum Kauf von 25 neuen Aktien benötigt man 29 Bezugsrechte.
Aber mein Verständnis der Aufgaben ist so, dass man einen Aktionär vor und nach der Kapitalerhöhung betrachten soll. Am 5.1. war sein Vermögen ein bestimmter Betrag x. Dann erfolgt die Kapitalerhöhung und am 8.1. hat er dann dadurch entweder einen Gewinn oder Verlust erlitten.
Zu 2g)
Der Unterschied dürfte durch die Art der Berechnung entstehen. Ich hab mit dem Wert von oben weitergerechnet. Da haben ich gez. Kapital durch die 2,56 € geteilt. Du hast vermutlich einfach die Anzahl der alten und neuen Aktien zusammengenommen und mit 1€ multipliziert.
Zu 3b/c/d)
Du vermischt hier ein paar Dinge. Bezugsrechte beziehen sich auf die Altaktien. Pro alter Aktie hat er ein Bezugsrecht. Aber zum Kauf von 25 neuen Aktien benötigt man 29 Bezugsrechte.
Aber mein Verständnis der Aufgaben ist so, dass man einen Aktionär vor und nach der Kapitalerhöhung betrachten soll. Am 5.1. war sein Vermögen ein bestimmter Betrag x. Dann erfolgt die Kapitalerhöhung und am 8.1. hat er dann dadurch entweder einen Gewinn oder Verlust erlitten.
Zuletzt bearbeitet:
3 b-dAn Investition sitze ich gerade dran. Hoffentlich kriege ich das heute fertig.
Zu 2g)
Der Unterschied dürfte durch die Art der Berechnung entstehen. Ich hab mit dem Wert von oben weitergerechnet. Da haben ich gez. Kapital durch die 2,56 € geteilt. Du hast vermutlich einfach die Anzahl der alten und neuen Aktien zusammengenommen und mit 1€ multipliziert.
Zu 3b/c/d)
Du vermischt hier ein paar Dinge. Bezugsrechte beziehen sich auf die Altaktien. Pro alter Aktie hat er ein Bezugsrecht. Aber zum Kauf von 25 neuen Aktien benötigt man 29 Bezugsrechte.
Aber mein Verständnis der Aufgaben ist so, dass man einen Aktionär vor und nach der Kapitalerhöhung betrachten soll. Am 5.1. war sein Vermögen ein bestimmter Betrag x. Dann erfolgt die Kapitalerhöhung und am 8.1. hat er dann dadurch entweder einen Gewinn oder Verlust erlitten.
Hört sich schlüssig an. Ich rechne nochmal neu. Lieben Dank
Hier mal mein Gedankengut zu Investition bisher.
Aufgabe 1
a)
Vorüberlegungen:
Mit der internen Zinsfußmethode ergibt sich für die Investition:
r = ( e1 / a0 ) - 1 = ( 990 € / 600 € ) - 1 = 0,65 ≙ 65 %
Sachinvestitionen deren Zins über dem Kapitalmarktzins (hier 10%) liegen werden immer vollständig ausgeführt. Es gibt nur dieses eine vorteilhafte Projekt für 600 €. Somit ist das optimale Sachinvestitionsvolumen a0 = 600 €.
b)
Kapitalwert (in €):
C = −600 + 990 * 1,1−1 = 300
C > 0
Die Sachinvestition ist vollständig vorteilhaft und wird somit vollständig durchgeführt.
Zinsgerade:
C1 = 990 – 1,1 * ( C0 – 400 ) = 1430 – 1,1 * C0
Für C1 = 0:
0 = 1430 – 1,1 * C0 | + 1,1 * C0
1,1 * C0 = 1430 | / 1,1
C0 = 1430 / 1,1 = 1300
Durch den Finanzmarkt kann ein Kredit aufgenommen werden, welcher später durch die Investition getilgt werden kann. Der mögliche maximale Verbrauch in t = 0 wäre somit 1300 €.
c)
Nutzen:
U = C0 * C1
= C0 * ( 1430 – 1,1 * C0 )
= 1430 * C0 – 1,1 * C02
U’= 1430 – 2,2 * C0 = 0
1430 – 2,2 * C0= 0 | - 1430
-2,2 * C0= - 1430| / -2,2
C0= - 1430 / -2,2 = 650
C0 in C1:
C1 = 1430 – 1,1 * 650 = 715
Maximaler Nutzen:
U = C0 * C1 = 650 * 715 = 464750
d)
Konsumplan:
t = 0:
C0 = liquide Mittel - Investitionssumme + Kredit
C0 = 1000 - 600 + Kredit = 650 –> Kredit = 250
t = 1:
C1 = Investitionsrückzahlung - Kredit - Zinsen
C1 = 990 – 250 – Zinsen = 715 –> Zinsen = 250 * 0,1 = 25
Aufgabe 1
a)
Vorüberlegungen:
- Konsum nur in t = 0
→ C0 = 1.000 und C1 = 0 - Investor erbringt Einlage; Konsum in t = 0 und t = 1
→ C0 = 1.000 – 600 = 400 und C1 = 990 - Konsum nur in t = 1
→ C0 = 0 und C1 = 990 + 400 * 1,1 = 1.430
C0 | C1 |
1.000 | 0 |
400 | 990 |
0 | 1.430 |
Mit der internen Zinsfußmethode ergibt sich für die Investition:
r = ( e1 / a0 ) - 1 = ( 990 € / 600 € ) - 1 = 0,65 ≙ 65 %
Sachinvestitionen deren Zins über dem Kapitalmarktzins (hier 10%) liegen werden immer vollständig ausgeführt. Es gibt nur dieses eine vorteilhafte Projekt für 600 €. Somit ist das optimale Sachinvestitionsvolumen a0 = 600 €.
b)
Kapitalwert (in €):
C = −600 + 990 * 1,1−1 = 300
C > 0
Die Sachinvestition ist vollständig vorteilhaft und wird somit vollständig durchgeführt.
Zinsgerade:
C1 = 990 – 1,1 * ( C0 – 400 ) = 1430 – 1,1 * C0
Für C1 = 0:
0 = 1430 – 1,1 * C0 | + 1,1 * C0
1,1 * C0 = 1430 | / 1,1
C0 = 1430 / 1,1 = 1300
Durch den Finanzmarkt kann ein Kredit aufgenommen werden, welcher später durch die Investition getilgt werden kann. Der mögliche maximale Verbrauch in t = 0 wäre somit 1300 €.
c)
Nutzen:
U = C0 * C1
= C0 * ( 1430 – 1,1 * C0 )
= 1430 * C0 – 1,1 * C02
U’= 1430 – 2,2 * C0 = 0
1430 – 2,2 * C0= 0 | - 1430
-2,2 * C0= - 1430| / -2,2
C0= - 1430 / -2,2 = 650
C0 in C1:
C1 = 1430 – 1,1 * 650 = 715
Maximaler Nutzen:
U = C0 * C1 = 650 * 715 = 464750
d)
Konsumplan:
t = 0:
C0 = liquide Mittel - Investitionssumme + Kredit
C0 = 1000 - 600 + Kredit = 650 –> Kredit = 250
t = 1:
C1 = Investitionsrückzahlung - Kredit - Zinsen
C1 = 990 – 250 – Zinsen = 715 –> Zinsen = 250 * 0,1 = 25
Anhänge
Investition
Aufgabe 2
a)
KE 1 auf S. 47
b)
Analog KE 2 auf S. 39
A ( -1700, 220, 605, 1331 )
r* = 0,1 d.h. der interne Zinsfuß der Zahlungsreihe der Investition a1 beläuft sich auf 10%.
Der Kapitalwert bei einem Kalkulationszinsfuß von Null (der Ordinatenwert bei r = 0) gibt die Summe der nicht abgezinsten Zahlungssalden einer Investition, ihren Nominalwert, wieder.
K = -1700 + 220 + 605 + 1331 = 456
Der Kapitalwert einer Normalinvestition konvergiert für r → ∞ gegen e0, da die nachfolgenden Zahlungsüberschüsse durch die Diskontierung immer weniger „ins Gewicht fallen“.
Im ökonomisch schwer interpretierbaren Bereich negativer Kalkulationszinsfüße hingegen strebt der Kapitalwert für r → –1 gegen unendlich.
Aufgabe 2
a)
KE 1 auf S. 47
b)
Analog KE 2 auf S. 39
A ( -1700, 220, 605, 1331 )
r* = 0,1 d.h. der interne Zinsfuß der Zahlungsreihe der Investition a1 beläuft sich auf 10%.
Der Kapitalwert bei einem Kalkulationszinsfuß von Null (der Ordinatenwert bei r = 0) gibt die Summe der nicht abgezinsten Zahlungssalden einer Investition, ihren Nominalwert, wieder.
K = -1700 + 220 + 605 + 1331 = 456
Der Kapitalwert einer Normalinvestition konvergiert für r → ∞ gegen e0, da die nachfolgenden Zahlungsüberschüsse durch die Diskontierung immer weniger „ins Gewicht fallen“.
Im ökonomisch schwer interpretierbaren Bereich negativer Kalkulationszinsfüße hingegen strebt der Kapitalwert für r → –1 gegen unendlich.
Anhänge
Zuletzt bearbeitet:
Investition
Aufgabe 3
3a)
( -2000, 960, 1296 )
i = 10 %
Kapitalwert:
K =
K = -2000 + 960 * 1,1-1 + 1296 * 1,1-2
= -2000 + 960 / 1,1 + 1296 / 1,12
= -56,1983
Die Investition ist nicht vorteilhaft, da sich ein negativer Kapitalwert ergibt.
EW = 1296 + 960 * 1,1 = 2352
KFinanz = EW / 1,12 = 2352 / 1,12 = 1943,8017
Entspricht e0 – K = 2000 – 56,1983 = 1943,8017.
Alternativ hätte man 1943,8017 in eine Finanzanlage zu 10 % Zinsen anlegen können.
3b) KE 2 S. 9
Für Investitionen, bei denen auf eine Anfangsauszahlung nur noch Einzahlungsüberschüsse folgen, ist der Kapitalwert im Bereich r > –1 eine stetige, streng monoton fallende Funktion des Kalkulationszinsfußes. Allgemein werden Investitionen, deren Zahlungsreihen einen einmaligen Vorzeichenwechsel von – nach + aufweisen, als Normalinvestitionen bezeichnet.
3c) KE 2 S.42
e0 + e1 * (1 + r)-1 + e2 * (1+r)-2 = 0
r1,2 =
=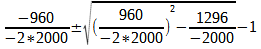
= 0,24 ± 0,84 – 1
r1= 0,08
r2= -1,6 → nicht relevant
Somit ist der interne Zins der Sachinvestition bei 8%. Da r1 < i, ist die Investition geringer verzinst als die Kapitalanlage. Eine Durchführung der Investition ist nicht vorteilhaft.
3d) KE 2 S. 32
Die Annuität charakterisiert die Zahlungsreihe durch eine rechnerische auf den Investitionszeitraum bezogene Zahlungsgröße. Da der Kapitalwert der Investition und der Kapitalwert der Zahlungsreihe aus T Annuitätszahlungen gleich hoch sind, bedeutet dies, dass der Investor bei Durchführung der Investition das gleiche Endvermögen erreicht, das er erreichen würde, wenn er die Unterlassensalternative wählte und ihm zusätzlich in allen Zeitpunkten t = 1, 2,..., T zusätzlich ein Betrag in Höhe der äquivalenten Annuität e* zur Verfügung gestellt würde.
Aufgabe 3
3a)
( -2000, 960, 1296 )
i = 10 %
Kapitalwert:
K =
K = -2000 + 960 * 1,1-1 + 1296 * 1,1-2
= -2000 + 960 / 1,1 + 1296 / 1,12
= -56,1983
Die Investition ist nicht vorteilhaft, da sich ein negativer Kapitalwert ergibt.
EW = 1296 + 960 * 1,1 = 2352
KFinanz = EW / 1,12 = 2352 / 1,12 = 1943,8017
Entspricht e0 – K = 2000 – 56,1983 = 1943,8017.
Alternativ hätte man 1943,8017 in eine Finanzanlage zu 10 % Zinsen anlegen können.
3b) KE 2 S. 9
Für Investitionen, bei denen auf eine Anfangsauszahlung nur noch Einzahlungsüberschüsse folgen, ist der Kapitalwert im Bereich r > –1 eine stetige, streng monoton fallende Funktion des Kalkulationszinsfußes. Allgemein werden Investitionen, deren Zahlungsreihen einen einmaligen Vorzeichenwechsel von – nach + aufweisen, als Normalinvestitionen bezeichnet.
3c) KE 2 S.42
e0 + e1 * (1 + r)-1 + e2 * (1+r)-2 = 0
r1,2 =
=
= 0,24 ± 0,84 – 1
r1= 0,08
r2= -1,6 → nicht relevant
Somit ist der interne Zins der Sachinvestition bei 8%. Da r1 < i, ist die Investition geringer verzinst als die Kapitalanlage. Eine Durchführung der Investition ist nicht vorteilhaft.
3d) KE 2 S. 32
Die Annuität charakterisiert die Zahlungsreihe durch eine rechnerische auf den Investitionszeitraum bezogene Zahlungsgröße. Da der Kapitalwert der Investition und der Kapitalwert der Zahlungsreihe aus T Annuitätszahlungen gleich hoch sind, bedeutet dies, dass der Investor bei Durchführung der Investition das gleiche Endvermögen erreicht, das er erreichen würde, wenn er die Unterlassensalternative wählte und ihm zusätzlich in allen Zeitpunkten t = 1, 2,..., T zusätzlich ein Betrag in Höhe der äquivalenten Annuität e* zur Verfügung gestellt würde.
Kann ihr jemand gute Nachhilfelehrer*innen empfehlen?
Würde mich bzgl. Nachhilfe anschließen, falls man die Stunden z.B. über Zoom gemeinsam nehmen könnte.Kann ihr jemand gute Nachhilfelehrer*innen empfehlen?


