Sonstige Aufgaben Statistik - Knifflige Aufgaben

Hallo, habe das Skript nahezu durch und zu drei Übungsaufgaben (ausgewählt wg. mgl. Klausurrelevanz) dürste ich nach Unterstützung

Abschnitt 14.11. Faktoren-Analyse - S. 381 Übung
Zeigen Sie, dass Eigenvektoren v1, v2 orthonormiert sind. Habe da keinen wirklichen Plan
Frage am Rande, wie spricht man eigentlich das zugehörige Symbol (siehe u. a. S. 375) aus?

Abschnitt 15.6.1 Item-Analyse - S. 422 Übung 15.2
Trennschärfe Corr (Xi, X) berechnen Kann ich dies anhand der Daten (überhaupt) manuell rechnen?

Abschnitt 15.7.5 Regression - S. 439 Übung 15.6
Prüfen Sie, ob sich die Achsenabschnitte und Steigungen in den durch ALTNEU = 0/1 def. Gruppen signifikant unterscheiden.
Die Stichprobengrößen der Gruppen sind N0 = 146, N1 = 204, N2 = 350.
Steigung Regressionsgeraden: ß0 = 0.446 (0.069), ß1 = 0.582 (.058),
Achsenabschnitte: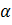 0 = 0.278 (0.061), 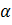1 = -0.241 (0.063) Standardabweichung in Klammer

Bei Anwenden der Formel 4 von Seite 106 komme ich auf sehr niedrige geschätzte Standardabweichungen (jeweils rd. 0,007) und in der Folge auf zweistellige Prüfgrößen (-19,41, 77,46). Unterliege ich da einem Denkfehler?

Mir ist klar, dass Kap. 15 nicht explizit für die Klausur zu beherrschen ist, allerdings sehe ich es als Übungsaufgaben zu den in Kap. 14 vorkommenden Inhalten und folglich kann das kommen.
Danke vorab für eure Antworten!

S.381

ist das kleine psi des griechischen Alphabets (sieht je nach Schriftart manchmal auch etwas anders aus). Die Vektoren stehen orthogonal (senkrecht aufeinander), wenn deren Skalarprodukt = 0 ist, also , und sind zusätzlich orthonormal wenn deren Länge 1 ist ( , analog für den zweiten)

S.422 Nicht 100%ig sicher, aber die Trennschärfe müsste die Korrelation zwischen den auserwählten Faktoren und den übrig gebliebenen sein. Da nur ein Faktor auserwählt wurde (KORIENT) ist die Trennschärfe zu Item(Faktor) 2 und 3 aus der Inter-Item-Korrelationsmatrix (Abb. 15.17) direkt auslesbar.

S.439 Alles richtig, da die Prüfgrößen (19.4 / 77.5) den kritischen Wert überschreiten (3,00 z.b. zum Niveau 0,27 %) muss die Nullhypothese (Mittelwerte unterscheiden sich nicht / delta =0) verworfen werden, damit signifikant verschieden.

Hallo Wesen,

vorne weg vielen herzlichen Dank! Man merkt, dass du im Thema drinnen bist

- S. 422: Der erste Satz stimmt jedenfalls. Für mich bleibt allerdings die Frage, wenn man Faktor 1 (KORIENT) auswählt und die Korrelation zum Gesamtwert der Skala sucht, was ist konkret zu rechnen?

Die Inter-Item-Korrelationsmatrix besagt ja nach meinem Verständnis, dass z. B. die Korrelation zw. KORIENT und KZWANG 0,26 (KPRIVAT 0,258) beträgt. Wie lässt sich das auf den Gesamtwert KORIENT vgl. mit KZWANG UND KPRIVAT umlegen? Addieren der beiden Werte (0,26 + 0,258) würde unterstellen, dass je mehr Faktoren, desto höher die Korrelation zw. einem Faktor und dem Gesamtwert.

- S. 439/441: Die "Alternativlösung" auf S. 441, welche zw. Mittelwertsverschiebungen signifikant ( 1 = 0 ablehnen) und Schereneffekt/Steigung der Regressionsgeraden nicht signifikant (ß1 = 0 beibehalten) unterscheidet, deutet für mich daraufhin, dass auch die Berechnung des t-Tests für ß ein anderes Ergebnis ("nicht signifikant") liefern sollte.

Was meinst du?

Hallo nochmal,

S. 422 Die Skala auf einen Faktor zur beschränken war vielleicht von mir etwas zu einfach gedacht. Gesucht sind dann unter anderem wohl Korr(X1, X)=Korr(X1, X2+X3). Mein Ansatz über 12.14 (S.257) dafür wäre

mit den Formeln 18.40 und 18.42 aus Seite 522.
Die Kovarianzen dürften sich wieder rückwärts über 12.14 bestimmen und man erhält das Konstrukt


Edit: Auf Seite 424 wird dann nochmal die Trennschärfe gesucht, diesmal bei 4 Items. Da bin ich mir dann nicht ganz sicher ob sich das so einfach übertragen lässt. Darum mal ein leichtes Fragezeichen dahinter.

S. 439/441 Das könnte daran liegen, dass dort die Gruppen ( Alt / Neu) nicht mehr getrennt betrachtet werden, sondern in einer Regressionsfunktion bestimmt werden. Die Standardfehler sind im Vergleich auch angestiegen, so dass das die Abweichungen in der Signifikanz erklären könnte.Muss ich aber nochmal drüber nachdenken :P

Nachtrag:
Die Formel für S.422 lässt sich wohl problemlos auf mehr als 3 Items erweitern, artet aber in Rechenarbeit aus :

Wenn die Kovarianzen gegeben sind wie z.B. auf Seite 361, dann erhält man darüber :


Das deckt sich mit der Angabe Korrigierte Item-Skala-Korrelation für ZGESAMT auf Seite 362.

Da schließe ich mich doch mal an.

Habt ihr die Lösung für Übung 3.1 auf S. 96?

Keiner?