- Hochschulabschluss
- Bachelor of Science
- 2. Hochschulabschluss
- Master of Science
- Studiengang
- M.Sc. Wirtschaftswissenschaft
- ECTS Credit Points
- 60 von 120
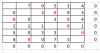
Ich kriege mit der ungarischen Methode gerade die Krise. Bei der Übungsaufgabe 2.6 komme ich von der Kostenmatrix C nicht auf die in der Lösung dargestellte reduzierte Kostenmatrix. Irgendwo habe ich einen Denkfehler und ich würde mich freuen, wenn mir jemand den Weg vom Schlauch weist  Danke!
Danke!
Anbei mein Rechenweg:
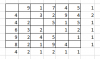
Ausganspunkt "Übung_26_1" mit Angabe der Zeilen- und Spaltenminima
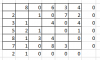
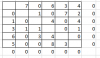
Zeilenminima abziehen "Übung_26_Z1" und dann Spalteminima abziehen "Übung_26_S2"
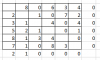
Alternative: Start mit Abzug der Spalteminima "Übung_26_S1", danach keine Zeilenminima zur Bearbeitung übrig.
Anbei mein Rechenweg:
Ausganspunkt "Übung_26_1" mit Angabe der Zeilen- und Spaltenminima
Zeilenminima abziehen "Übung_26_Z1" und dann Spalteminima abziehen "Übung_26_S2"
Alternative: Start mit Abzug der Spalteminima "Übung_26_S1", danach keine Zeilenminima zur Bearbeitung übrig.